Last Updated on December 18, 2021
The average, also known as the arithmetic average or the mean of a set of values is a nice and simple number that is easy to calculate and interpret. However, it not valid under all circumstances and must be used with caution.
Given a set of numbers, we cannot blindly calculate the average – take the sum of the numbers and divided by the number of items in the set. I am guilty of doing this too.
What does the average represent?
Consider a set of students and the marks they have got. What does the average mark represent? The typical performance of the class? Yes, if most people got a mark close to the average? Then we could talk about above-average and below-average?
Yes, but under certain circumstances.
The bell curve
Most of us would have encountered the bell curve at some stage in life – eg. performance based increments. It is a probability distribution that has a peak and is symmetric on either side of the peak.
The peak represents the average and the fatness of the curve or the spread the standard deviation. These two quantities are derived from the probability distribution.
Yes, the arithmetic mean is a derived quantity. No one just came up with its formula.
The point is that the arithmetic mean is valid only for such symmetric distribution. So is the idea of standard distribution.
Mutual Fund Star Ratings are flawed!
Mutual fund risk and returns (or any security for that matter) are not normal. This automatically means quantities like alpha, beta, sharpe, Sortino etc are not valid. And in turn, means star ratings which use these metrics are not valid.
Mutual Fund Category Average
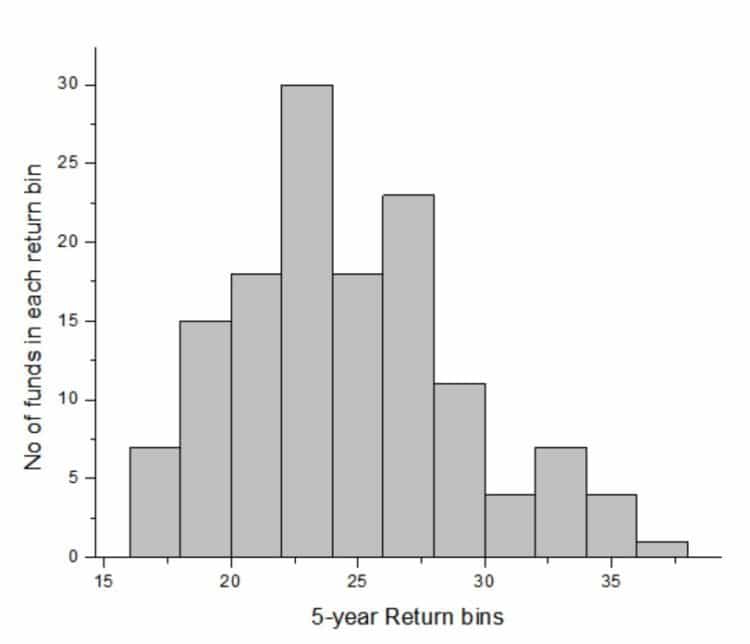
To elaborate the above point, consider the 5-year return distribution of multi-cap funds.
It should be immediately obvious that the distribution is not symmetric. Therefore a typical or average return is not of much use as it does not divide the distribution equally.
In fact, one should not even calculate the average in such a case.
Instead of the average one should use the median. This is a quantity that divides the distribution in half – 50% above the median and 50% below. For a bell curve, the average = median.
The median is also known as the second quartile. Any return above the median return falls in the top 50%.
One can also use the third quartile – top 75% of returns.
The whole point of this post is to suggest using the median and/or3rd quartile instead of the mean. The mean is “typically” invalid.
As mentioned above, I am guilty of using the category average returns too. I have now updated the mutual fund screener with median return instead of the mean.
About The Author
Dr M. Pattabiraman(PhD) is the founder, managing editor and primary author of freefincal. He is an associate professor at the Indian Institute of Technology, Madras. He has over nine years of experience publishing news analysis, research and financial product development. Connect with him via Twitter or Linkedin or YouTube. Pattabiraman has co-authored three print books: (1) You can be rich too with goal-based investing (CNBC TV18) for DIY investors. (2) Gamechanger for young earners. (3) Chinchu Gets a Superpower! for kids. He has also written seven other free e-books on various money management topics. He is a patron and co-founder of “Fee-only India,” an organisation to promote unbiased, commission-free investment advice.Use our Robo-advisory Excel Template for a start-to-finish financial plan! Now with a new demo video! ⇐ More than 800 investors and advisors use this!
Our flagship course! Learn to manage your portfolio like a pro to achieve your goals regardless of market conditions! ⇐ More than 2700 investors and advisors are part of our exclusive community! Get clarity on how to plan for your goals and achieve the necessary corpus no matter what the market condition is!! Watch the first lecture for free! One-time payment! No recurring fees! Life-long access to videos! Reduce fear, uncertainty and doubt while investing! Learn how to plan for your goals before and after retirement with confidence.
Our new course! Increase your income by getting people to pay for your skills! ⇐ More than 620 salaried employees, entrepreneurs and financial advisors are part of our exclusive community! Learn how to get people to pay for your skills! Whether you are a professional or small business owner who wants more clients via online visibility or a salaried person wanting a side income or passive income, we will show you how to achieve this by showcasing your skills and building a community that trusts you and pays you! (watch 1st lecture for free). One-time payment! No recurring fees! Life-long access to videos!
My new book for kids: “Chinchu gets a superpower!” is now available!
Must-read book even for adults! This is something that every parent should teach their kids right from their young age. The importance of money management and decision making based on their wants and needs. Very nicely written in simple terms. - Arun.Buy the book: Chinchu gets a superpower for your child!
How to profit from content writing: Our new ebook for those interested in getting side income via content writing. It is available at a 50% discount for Rs. 500 only!
Want to check if the market is overvalued or undervalued? Use our market valuation tool (will work with any index!), or you buy the new Tactical Buy/Sell timing tool!
We publish mutual fund screeners and momentum, low volatility stock screeners .every month.
About freefincal & its content policy Freefincal is a News Media Organization dedicated to providing original analysis, reports, reviews and insights on developments in mutual funds, stocks, investing, retirement and personal finance. We do so without conflict of interest and bias. Follow us on Google News. Freefincal serves more than three million readers a year (5 million page views) with articles based only on factual information and detailed analysis by its authors. All statements made will be verified from credible and knowledgeable sources before publication. Freefincal does not publish any paid articles, promotions, PR, satire or opinions without data. All opinions presented will only be inferences backed by verifiable, reproducible evidence/data. Contact information: letters {at} freefincal {dot} com (sponsored posts or paid collaborations will not be entertained)
Connect with us on social media
- Twitter @freefincal
- Subscribe to our Youtube Videos
- Posts feed via Feedburner.
Our publications
You Can Be Rich Too with Goal-Based Investing
Published by CNBC TV18, this book is meant to help you ask the right questions, seek the correct answers, and since it comes with nine online calculators, you can also create custom solutions for your lifestyle! Get it now. It is also available in Kindle format.Gamechanger: Forget Startups, Join Corporate & Still Live the Rich Life You Want
This book is meant for young earners to get their basics right from day one! It will also help you travel to exotic places at a low cost! Get it or gift it to a young earner.Your Ultimate Guide to Travel
This is an in-depth dive analysis into vacation planning, finding cheap flights, budget accommodation, what to do when travelling, how travelling slowly is better financially and psychologically with links to the web pages and hand-holding at every step. Get the pdf for Rs 199 (instant download)Free android apps
- All calculators from our book, “You can be Rich Too” are now available on Google Play!
- Install the Financial Freedom App! (Google Play Store)
- Install Freefincal Retirement Planner App! (Google Play Store)
- Find out if you have enough to say "goodbye" to your employer (Google Play Store)