Last Updated on December 28, 2021 at 6:31 pm
SEBI’s Mutual Fund Scheme Categorization requires fund houses to use a term known as Macaulay Duration to differentiate among debt mutual funds. Here is a simple explanation of what is Macaulay Duration and the more important modified duration and why you need to understand their significance if your mutual fund invests in bonds (debt mutual funds, hybrid funds, asset-allocation funds, balanced funds).
Here is a discussion on the pros and cons of SEBI’s Mutual Fund Scheme Categorization. If debt mutual funds are new to you, here is a simple explanation: What is a Debt Mutual Fund?
Download free e-book: A Beginner’s Guide To Investing in Debt Mutual Funds
Please note that the following is an extremely simple account of duration concepts meant for new mutual fund investors.
Join 32,000+ readers and get free money management solutions delivered to your inbox! Subscribe to get posts via email! (Link takes you to our email sign-up form)
🔥Want to create a complete financial plan? Learn goal-based investing? Exclusive access to our DIY tools? Increase your income with your skills? Enjoy massive discounts on our robo-advisory tool & courses! 🔥
What is “duration” in bond and debt mutual fund investing?
Duration is a measure of risk. The Macaulay Duration is a measure of how long it will take for you to recoup your investment (at the price that you purchased).
The modified duration is a measure of much the price of a bond and therefore the NAV of a debt mutual fund will change if interest rates change by 1%.
Why do bond prices vary in the market?
Simple demand and supply. If new bonds are available at higher interest rates, the demand for older bonds will decrease and they will have to be priced lower than their face value.
A bond initially priced ar Rs. 100 offering 10% interest rate will have an initial yield of
10/100 = 10%, where 10 is the interest paid out on the Rs. 100.
If newer bonds are available for 11%, the older bonds will have to be priced lower, say Rs. 90.
Then for a new buyer, the yield is 10/90 = 11.11%. So now the old bond is bit more attractive than the new 11% bonds.
That is, as the price drops, the bond yield increases and vice versa.
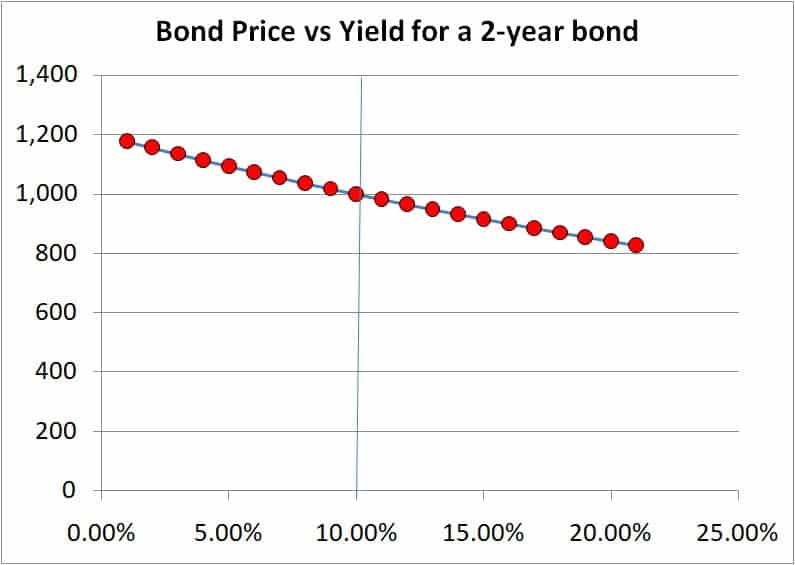
Price vs Yield for a short-term bond
This is the bond price vs yield for a two year bond with a 10% coupon rate. I shall not discuss the math behind this relationship here.
Price vs Yield for a long-term bond
Notice how the above graph changes when the duration is increased.
The two graphs illustrate why the idea of duration is important to debt mutual fund investors.
For a short-term bond, when the yields change (due to market supply vs demand), the corresponding price change is small and therefore the risk is also small.
For a long-term bond, the price change is a lot stronger or steeper (esp. towards lower yields). This is the reason why I keep saying stay away from dynamic bond funds and long-term gilts. If rates do not decrease or worse if rates start increasing after you buy such funds, you will see significant losses.
Duration is a measure of the risk in bond price
What is Macaulay Duration?
Let us find out with a series of examples.
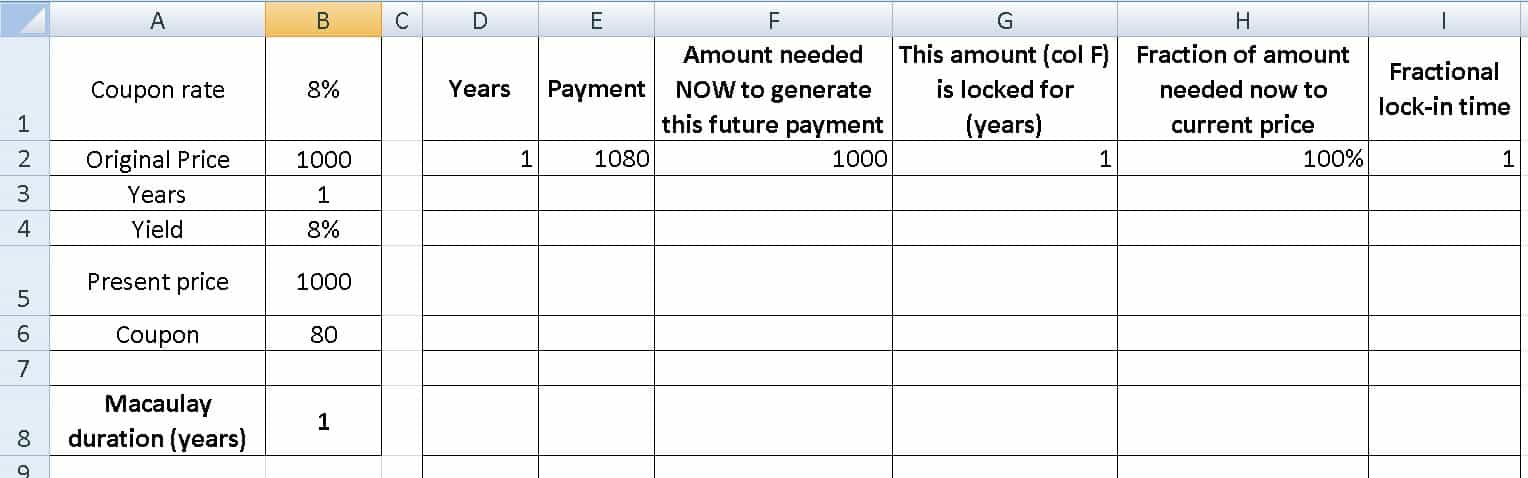
Suppose a Rs. 1000 bond was issued at a coupon rate (interest rate) of 8%. So Rs. 1000 is the original price of the bond and the interest payment each year is Rs. 80.
We wish to buy this bond and there is one more year for maturity. The current yield is 8% (same as original rate) and therefore the current price is also Rs. 1000.
After 1Y, the bond issuer will have to pay us Rs. 80 interest + the face value of Rs. 1000.
So now we ask, what is the amount needed to generate 1080 after 1Y?
The answer is 1080/(1+8%) = 1000, where 8% is the current yield of the bond.
The Macaulay duration is defined as the amount of time it takes to recoup our investment.
So we paid Rs. 1000 at a yield of Rs. 8%. This will be locked in for a year. So it will take one year to recoup the original investment. The Macaulay duration is 1 year. This is of course trivial. Please hang on. This situation is tabulated below.
Example 1:
Example 2:
Let consider the same bond but with two years to maturity and the current yield is 8% and therefore price is Rs. 1000.
After 1Y, we will receive the interest of Rs. 80. After 2Y: Rs 80 + Rs. 1000 = Rs. 1080.
Now out of the Rs. 1000 we paid, say
Rs. X will become Rs. 80 after 1Y at the current yield of 8%. X = 80/(1+8%) = Rs. 74.07
Rs. y will become Rs. 1080 after 2Y at the current yield of 8%.
Y = 1080/(1+8%)^2 = Rs. 925.93
Rs. X + Rs. Y = Rs. 1000 = amount we paid to buy the bond.
Let us look at this in another way.
X/1000 of the original investment will be locked in for 1Y, or
Rs. (X/1000) x 1 Year = Fractional lock-in period of Rs. X = 0.07 years (see table below)
In other words, if Rs. 1000 is locked in for one year, how long should Rs. X be locked in for the same yield in investment:
This is (X/1000) x 1 Year = 0.07 years
Similarly, Y/1000 for the original investment will be locked in for 2Y, or
Rs. (Y/1000) x 2 years = Fraction lock-in period of Rs. Y. =1.85 years
Or, If Rs. 1000 is locked in for two years, how long should Rs. Y be locked for the same yield in investment:
This is (Y/1000) x 2 Years 1.85 years
Macaulay Duration = 0.07 + 1.85 = sum of fractional lock-in periods = 1.93 years
That is, after 1.93 years, you would have effectively recouped your investment even though you will get your money back only after 2Y.
Example 3
One more example of a 5 year bond and the current yield is the same as coupon rate.
The Macaulay duration of 4.31 years = sum of entries in column I. That is the fractional lock-in periods for each payment.
Example 4:
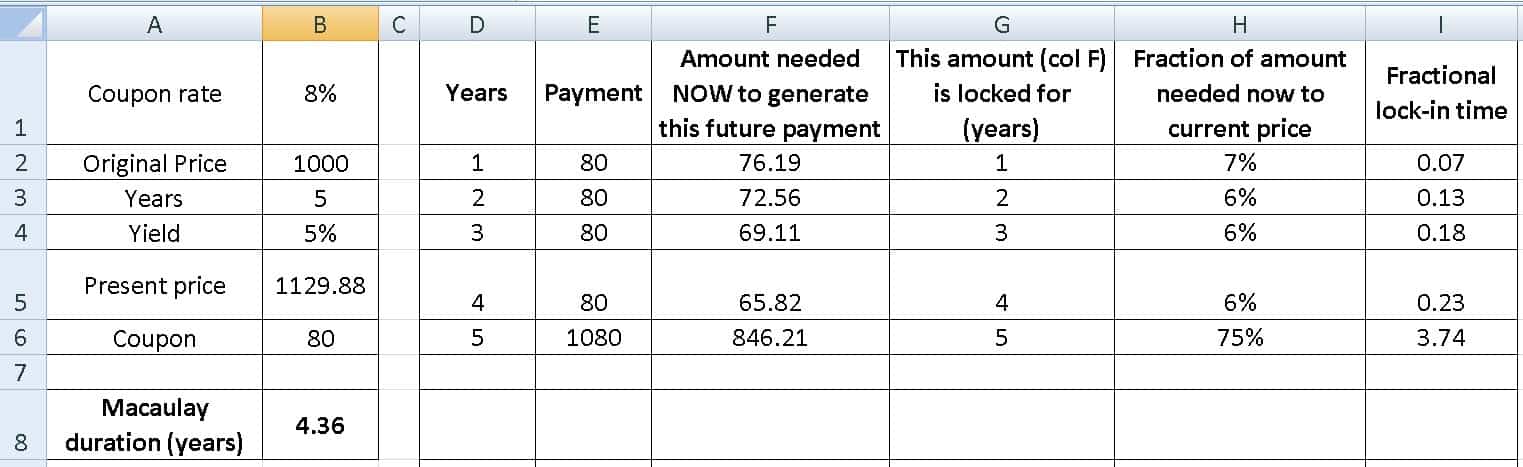
Now let us assume that the 5Y bond is available at a reduced yield of 5%. This means we have to pay more for the bond. It is more valuable.
The Macaulay duration has increased but only by a small amount. Note that 4.36 years is the time required to recoup the original investment of Rs. 1129.88.
Example 5:
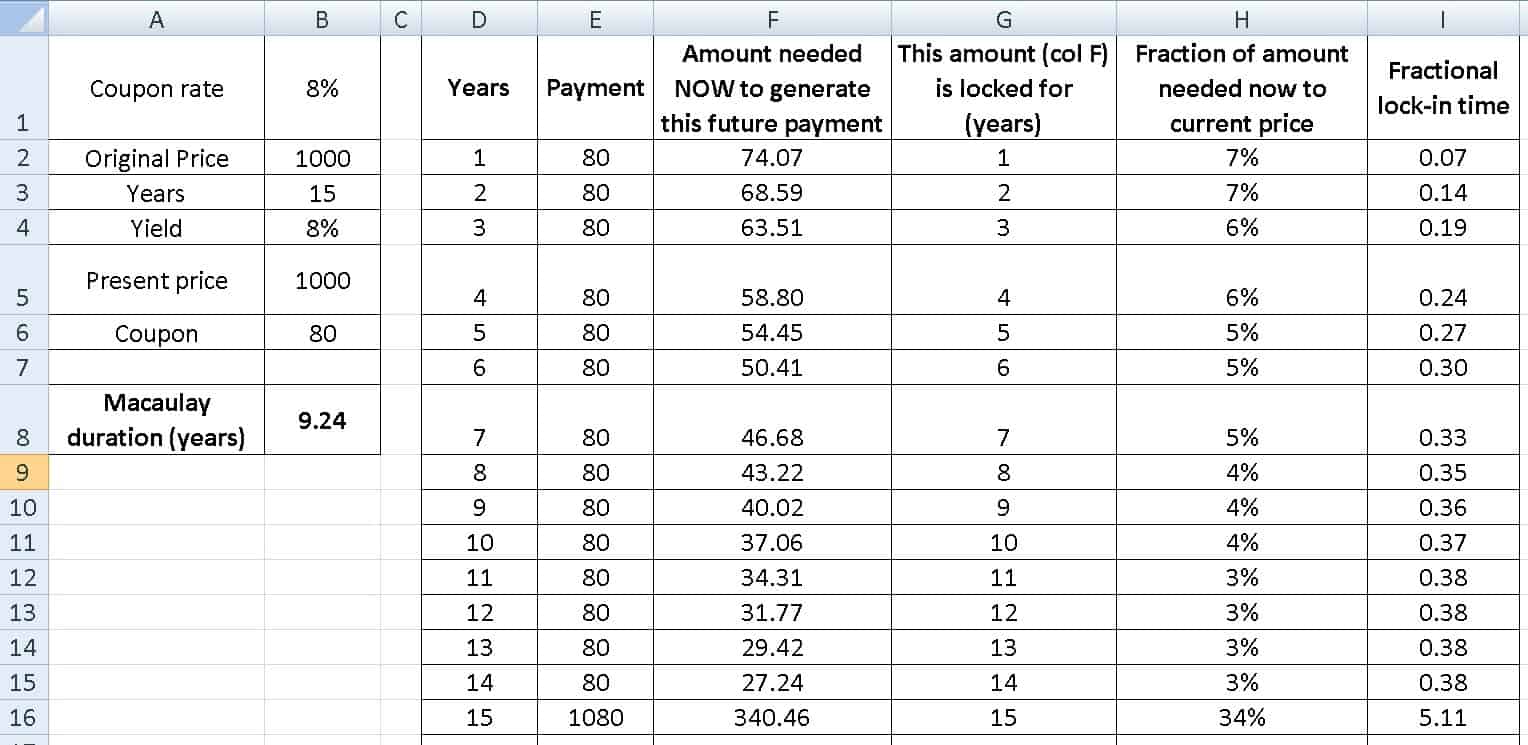
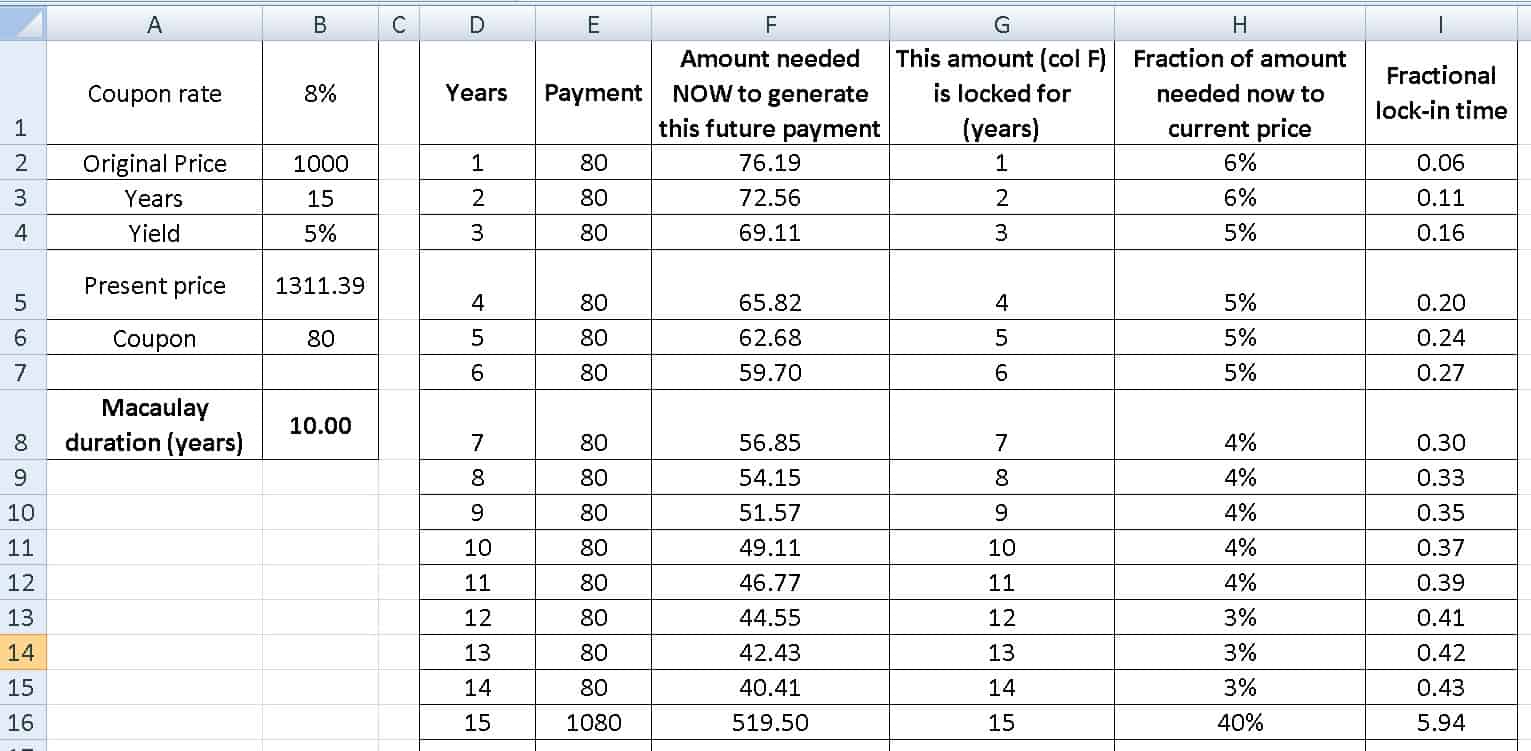
Now consider a 15-year bond with current yield the same as coupon rate.
Example 6:
Now if the yield was lower by 3% ==> 5%, the Macaulay duration is 10 years
If the tenure of the bond is increased by 3 times, its sensitivity to changes in yield increases by 7 times!
Higher the tenure of the bond, the more sensitive the Macaulay duration to changes in yield.
In fact, the sensitivity is rather less than what is actually seen. So to depict the price sensitivity to yield changes better, we need another measure the modified duration.
The modified duration is the rate at which the price changes with yield. With a little math (that we will spare ourselves from) we can show
Modified duration= Macaulay Duration/(1+ current yield) (for annual payments).
If you remember your school calculus
(Change in bond price)/(change in interest rate or yield) = rate of change
The Modified duration =-1 x (Change in bond price)/(change in interest rate or yield)
The negative sign is because the slope of the bond price vs bond yield curve (see above) is negative.
So we have,
(Change in bond price) = -1 x Modified Duration x (change in interest rate)
Change in NAV = -1 x Modified Duration x (change in interest rate)
If the modified duration is 5 years and if the interest rates have increased by 1%,
change in interest is +1% (it would be -1% if the rates had dropped by 1%)
So the change in bond price or NAV =(-1) x 5 x (+1%) = -5%
Higher the modified duration, higher the Macaulay duration, higher the sensitivity to interest rate movement. This sensitivity is for both corporate bonds and gilts: Debt Mutual Funds: Credit Risk and Interest Rate Risk Can Co-exist!
Do not invest in debt mutual funds without understanding risks! Download our free e-book: A Beginner’s Guide To Investing in Debt Mutual Funds
🔥Enjoy massive discounts on our courses, robo-advisory tool and exclusive investor circle! 🔥& join our community of 7000+ users!
Use our Robo-advisory Tool for a start-to-finish financial plan! ⇐ More than 2,500 investors and advisors use this!
Track your mutual funds and stock investments with this Google Sheet!
We also publish monthly equity mutual funds, debt and hybrid mutual funds, index funds and ETF screeners and momentum, low-volatility stock screeners.
- Do you have a comment about the above article? Reach out to us on Twitter: @freefincal or @pattufreefincal
- Have a question? Subscribe to our newsletter using the form below.
- Hit 'reply' to any email from us! We do not offer personalized investment advice. We can write a detailed article without mentioning your name if you have a generic question.
Join 32,000+ readers and get free money management solutions delivered to your inbox! Subscribe to get posts via email! (Link takes you to our email sign-up form)
About The Author
Dr M. Pattabiraman(PhD) is the founder, managing editor and primary author of freefincal. He is an associate professor at the Indian Institute of Technology, Madras. He has over ten years of experience publishing news analysis, research and financial product development. Connect with him via Twitter(X), Linkedin, or YouTube. Pattabiraman has co-authored three print books: (1) You can be rich too with goal-based investing (CNBC TV18) for DIY investors. (2) Gamechanger for young earners. (3) Chinchu Gets a Superpower! for kids. He has also written seven other free e-books on various money management topics. He is a patron and co-founder of “Fee-only India,” an organisation promoting unbiased, commission-free investment advice.Our flagship course! Learn to manage your portfolio like a pro to achieve your goals regardless of market conditions! ⇐ More than 3,000 investors and advisors are part of our exclusive community! Get clarity on how to plan for your goals and achieve the necessary corpus no matter the market condition is!! Watch the first lecture for free! One-time payment! No recurring fees! Life-long access to videos! Reduce fear, uncertainty and doubt while investing! Learn how to plan for your goals before and after retirement with confidence.
Our new course! Increase your income by getting people to pay for your skills! ⇐ More than 700 salaried employees, entrepreneurs and financial advisors are part of our exclusive community! Learn how to get people to pay for your skills! Whether you are a professional or small business owner who wants more clients via online visibility or a salaried person wanting a side income or passive income, we will show you how to achieve this by showcasing your skills and building a community that trusts and pays you! (watch 1st lecture for free). One-time payment! No recurring fees! Life-long access to videos!
Our new book for kids: “Chinchu Gets a Superpower!” is now available!
Must-read book even for adults! This is something that every parent should teach their kids right from their young age. The importance of money management and decision making based on their wants and needs. Very nicely written in simple terms. - Arun.Buy the book: Chinchu gets a superpower for your child!
How to profit from content writing: Our new ebook is for those interested in getting side income via content writing. It is available at a 50% discount for Rs. 500 only!
Do you want to check if the market is overvalued or undervalued? Use our market valuation tool (it will work with any index!), or get the Tactical Buy/Sell timing tool!
We publish monthly mutual fund screeners and momentum, low-volatility stock screeners.
About freefincal & its content policy. Freefincal is a News Media Organization dedicated to providing original analysis, reports, reviews and insights on mutual funds, stocks, investing, retirement and personal finance developments. We do so without conflict of interest and bias. Follow us on Google News. Freefincal serves more than three million readers a year (5 million page views) with articles based only on factual information and detailed analysis by its authors. All statements made will be verified with credible and knowledgeable sources before publication. Freefincal does not publish paid articles, promotions, PR, satire or opinions without data. All opinions will be inferences backed by verifiable, reproducible evidence/data. Contact information: To get in touch, use this contact form. (Sponsored posts or paid collaborations will not be entertained.)
Connect with us on social media
- Twitter @freefincal
- Subscribe to our YouTube Videos
- Posts feed via Feedburner.
Our publications
You Can Be Rich Too with Goal-Based Investing
Published by CNBC TV18, this book is meant to help you ask the right questions and seek the correct answers, and since it comes with nine online calculators, you can also create custom solutions for your lifestyle! Get it now.Gamechanger: Forget Startups, Join Corporate & Still Live the Rich Life You Want
This book is meant for young earners to get their basics right from day one! It will also help you travel to exotic places at a low cost! Get it or gift it to a young earner.Your Ultimate Guide to Travel
This is an in-depth dive into vacation planning, finding cheap flights, budget accommodation, what to do when travelling, and how travelling slowly is better financially and psychologically, with links to the web pages and hand-holding at every step. Get the pdf for Rs 300 (instant download)